行测中数量关系的题目是很多同学的痛难点,其实数量关系中包含有很多种题型,我们可以挑选当中难度系数相对低,容易得分的题型来做,和定最值问题就是我们首选中的一员。下面华图教育带大家来学习和定最值问题。
一、什么是和定最值问题
顾名思义,就是在和一定的条件下求解最值的问题。一般在题目中体现为已知若干个量的总和或平均数为定值,想求解其中某个量的最大值或最小值。此类题目的特征大家可以简记为五个字:和定,求最值。
二、解题原则
当几个量总和为定值的情况下,若想求其中某个量的最大值,则其他量应尽可能小;若想求其中某个量的最小值,则其他量应尽可能大。
三、经典例题
(一)求最大(小)量的最大(小)值
例1
六一儿童节期间,100名幼儿园学生参加5项活动,参加人数最多的活动人数不超过参加人数最少活动人数的2倍,则参加人数最少的活动最少有多少人参加?
A.10 B.11 C.12 D.13
【答案】C。
【华图解析】要使参加人数最少的活动的人数最少,则其他活动的参加人数应尽量多,即各项活动的人数尽量接近(可以相等),又已知参加人数最多的活动人数不超过参加人数最少活动人数的2倍,可用未知数表示如下,
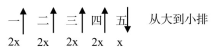
则有2x×4+x=100,解得x=11.X,x为整数,且所求为最小值,故向上取整,x=12,即参加人数最少的活动最少有12人参加,选择C项。
(二)求最大(小)量的最小(大)值
例2
现有25株树苗要分植于5片绿地上,若使每片绿地上分得的树苗数各不相同,则分得树苗最多的绿地至少可分得几株树苗?
A.8 B.7 C.6 D.5
【答案】B。
【华图解析】要使分得树苗最多的绿地分得的树苗数尽量少,则应使其他绿地分得的树苗数尽量多,即应与最多的尽量接近,则分别差1,用未知数表示如下,
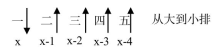
则有 x+x-1+x-2+x-3+x-4=25,解得 x=7,即分得树苗最多的绿地至少可分得7株,选择B项。
(三)求中间某个量的最大(小)值
例3
5人的体重之和是422斤,他们的体重都是整数,并且各不相同,最轻的人体重不低于70斤,则体重第三重的人最重可能是多少斤?
A.90 B.82 C.84 D.92
【答案】D。
【华图解析】要使第三重的人体重尽可能重,则其他人的体重应尽量轻,已知最轻的人体重不低于70斤,则第四和第五重的
人的体重分别为71和70斤,其余人的体重未知,用未知数表示如下,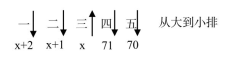
则有x+2+x+1+x+71+70=422,解得x=92.X ,体重为整数,所求为最大值,故应向下取整,即第三重的人体重最重为 92斤,选择D项。
以上就是对和定最值问题中基础题型的举例分析,华图教育希望大家后续多加练习快速掌握,为解决类似题目奠定基础。










