最值问题是行测数量关系能够拿分的一种简单题型。那么什么是和定最值呢?和定最值,顾名思义,即几个数的和是个定值,要求其中一个数的最大值或最小值。解决这种题的一原则就是要想其中一个数尽可能大/小,则其余的数尽可能的小/大。下面我们来从题中一起看看不同的和定最值问题如何求解。
例1
现有21本故事书要分给5个人阅读,如果每个人得到的数量均不相同,那么得到故事书数量最多的人最多可以得到( )本。
A.5 B.7 C.9 D.11
【答案与解析】D。21本书分给5个人阅读,即5个人分得的书本本数加和为21,要求分得数量最多的人最多可以得到多少本。由于总数就只有21,要想让分得数量最多的人最多,其他人都得越少越好。那么最少分多少呢?第一步进行排序,将5个人分到的数量从多到少依次排名为一二三四五。第二步依次表示出每个人分得的数量。由于每个人得到的数量均不相同,倒数第二、第三、第四的数量最少依次应为1、2、3、4。设数量最多的为x。得到如下表格:
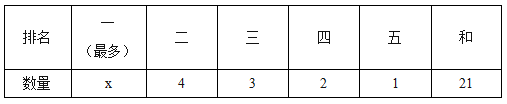
第三步列式子求解。根据总和为21列式可得:x+4+3+2+1=21。解得x=11,本题选D。
例2
现有21本故事书要分给5个人阅读,如果每个人得到的数量均不相同,那么得到故事书数量最多的人至少可以得到( )本。
A.5 B.7 C.9 D.11
【答案与解析】B。21本书分给5个人阅读,即5个人分得的书本本数加和为21,要求分得数量最多的人至少可以得到多少本。要想让分得数量最多的人最少,其他人都得越多越好。那么最多分多少呢?第一步进行排序,将5个人分到的数量从多到少依次排名为一二三四五。第二步依次表示出每个人分得的数量。设数量最多的为X,第二多的人想要尽可能多,那么就应该是刚好比数量最多的人只少一本;同理,第三多的人想要尽可能多,那么数量就应该是刚好比数量第二多的人只少一本。以此类推,我们可以得到以下表格。

第三步列式求解。根据加和一定(为21本),可得:x+(x-1)+(x-2)+(x-3)+(x-4)=21,解得x=6.2。即数量最多的至少有6.2本,已经是“至少”的情况了,方知不可能再比6.2本更少了,因此只能取7。选B。
搞懂以上两个题目之后,我们来总结一下和定最值问题的方法——第一步列表排序,第二步设未知数表示所有数量,第三步列式求解。
这个方法,在和定最值问题的求解过程中,无论是求最大(小)量的最大(小)值,最大(小)量的最小(大)值,还是中间量的最大(小)值;无论是几个数各不相同,还是可以相同,一般用到它来解出题目都没有问题。但有两点需要注意:第一点是避免定势思维。有些题目可能题中不会有“各数量各不一致”这种意思的条件,也就是5名同学的书本数量可以是相同。因此排序的时候考虑各次序的值是否可以相同,避免定势思维。第二点需要注意的是最后解方程解出来的结果如果不是整数,这个时候往往不能够四舍五入去进行取舍,大家记住四个字“代进去读”。即应该把求解出的小数代入求解的这句话去读,方可知进还是舍。比如已知5名同学总分并且均已及格,求问最高分最少是多少分。若我们设的第一名为x并求解为87.3,则我们代到句子里——即“第一名最少87.3”可知,不可能比87.3更少了,因此应该进位取88分。
华图教育希望通过本次的学习,能够攻克这种题型,见题即拿分。当然在实际考察过程中,也可能把和定最值和其他考点进行结合,无论怎样,和定最值这块都是万变不离其宗的,希望大家把和定最值的三步掌握在手、熟记在心。











